
 Natuurkunde 2025-2026
Natuurkunde 2025-2026- Verberg vooruitgang Hide progress Toon vooruitgang Show progress
- Verwijder je antwoorden (op deze pagina) Remove your answers (on this page)

 Natuurkunde 2025-2026
Natuurkunde 2025-2026Deze open-source cursus is in ontwikkeling. De aanbevelingen van leerlingen om
dit materiaal te verbeteren zijn erg welkom via info@wiskunde.opmaat.org
Dit kan gaan over:
Een hockeyschijf of puck krijgt op een bevroren vijver een horizontale slag waardoor hij met een snelheid van \(20\mathord {,}5\) \(\mathrm {m}/\mathrm {s}\) vertrekt. Na hoeveel meter komt de puck tot rust als de wrijvingsfactor tussen de puck en het ijs \(0\mathord {,}18\) bedraagt?
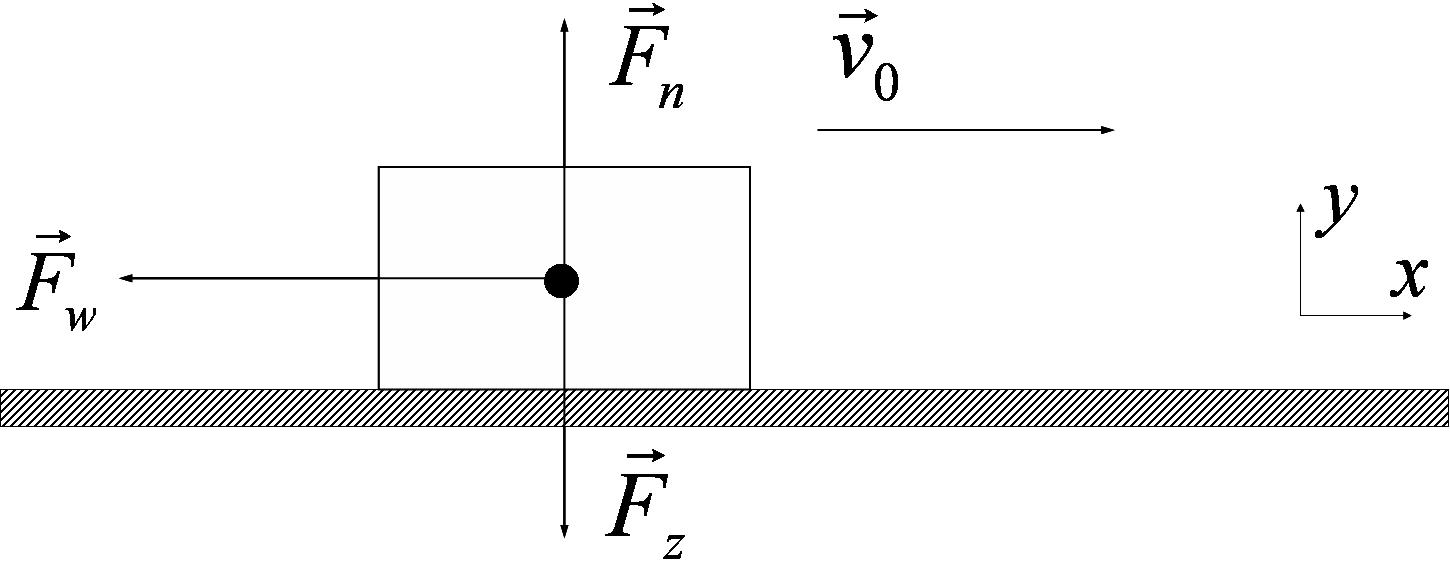
De tijd uit de vergelijkingen voor een EVRB elimineren, waarbij de eindsnelheid \(v\) en de beginpositie \(x_0\) nul zijn, levert:
Vergelijking (-v_0^2/2x) samen met (a) levert dan:
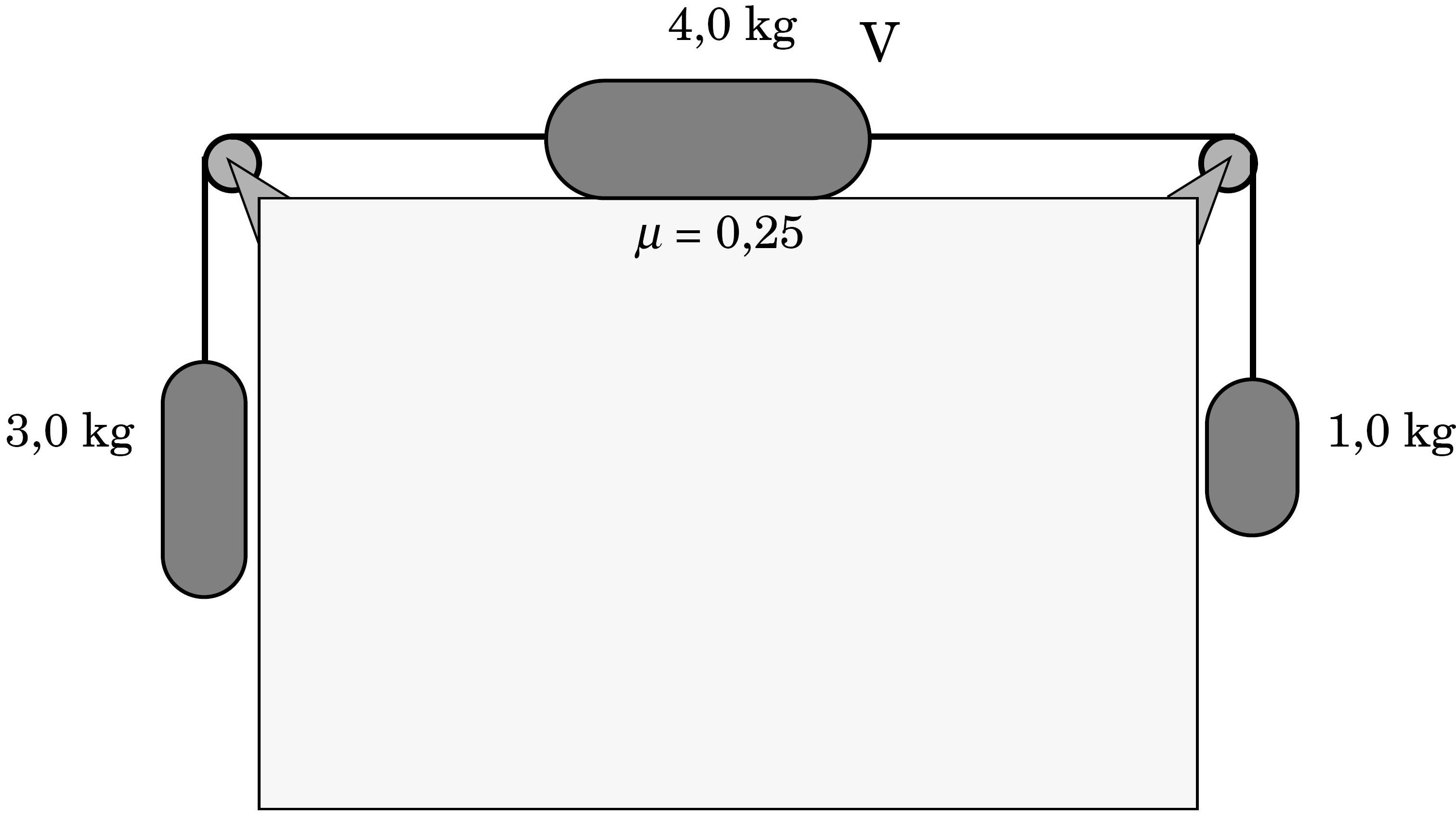
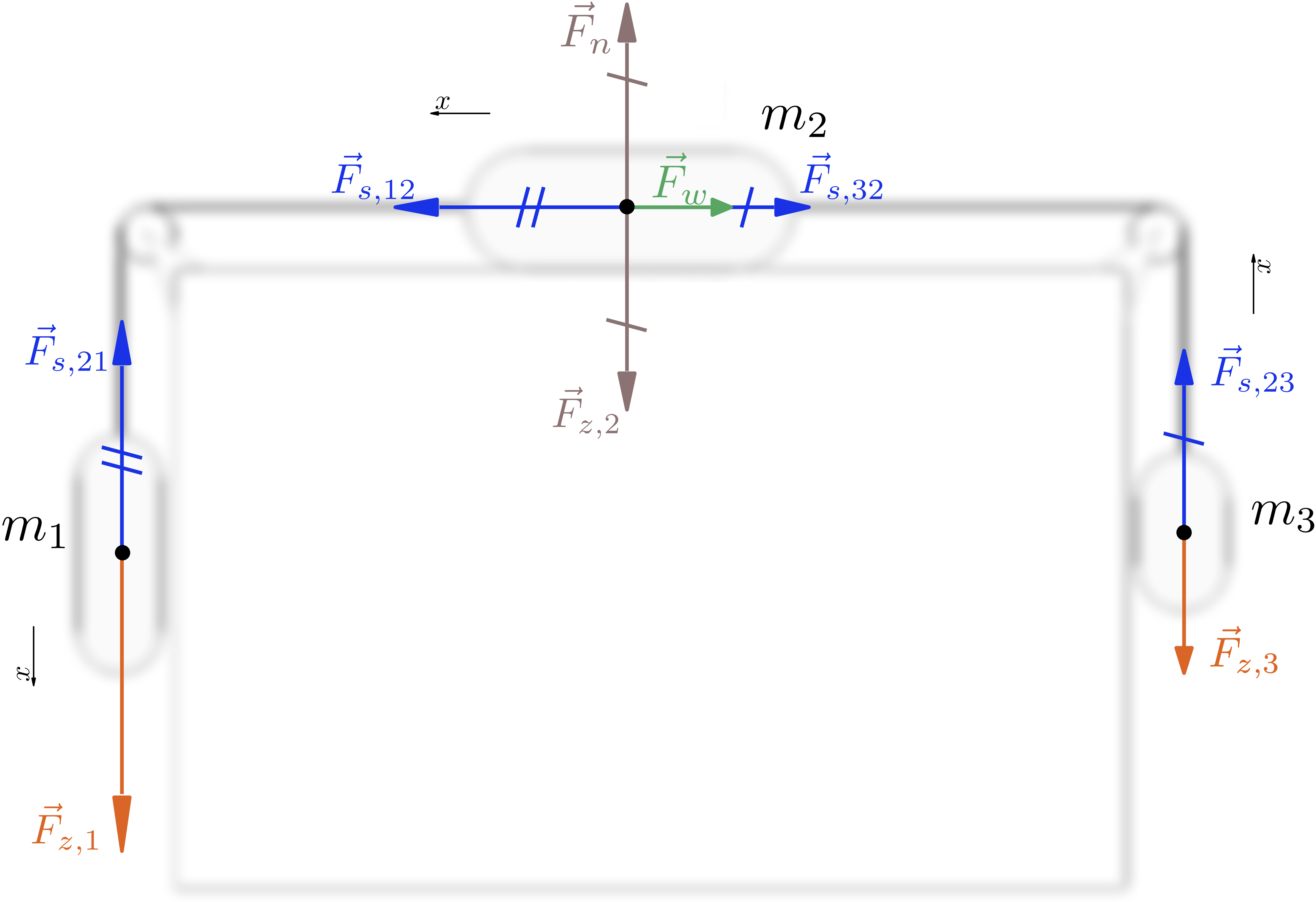
Voor \(m_3\) vinden we, met nu de keuze van de \(x\)-as verticaal naar boven:
Voor \(m_2\) vinden we, met de keuze van de \(x\)-as horizontaal naar links:
Volgens de derde wet van Newton kunnen we de overeenkomstige spankrachten aan mekaar gelijk stellen: \(F_{s,21}=F_{s,12}\) en \(F_{s,32}=F_{s,23}\). Samen met \(F_w=\mu F_n\) en \(F_z=ma\) hebben we drie vergelijkingen en drie onbekenden. Oplossen naar de versnelling levert:
Realiseer je dat de keuze van de \(x\)-as bij het bepalen van de componenten van de krachten de tekens bepalen van die componenten – en ook die van de versnelling. Als je bijvoorbeeld tweemaal \(a\) schrijft (in vergelijking (m_1) en (m_3)) moet het ook effectief over dezelfde versnelling gaan, en niet over versnellingen die elkaars tegengestelde zijn. Met de \(x\)-as verticaal naar beneden georiënteerd voor \(m_1\), zal de versnelling voor \(m_1\) positief zijn als de massa naar beneden versnelt (wat hij doet; \(m_1>m_3\)). Voor \(m_3\) moet je dan de \(x\)-as verticaal omhoog kiezen, wil je dat \(a\) evenzeer positief is of dus dezelfde betekenis heeft.
Merk ook op dat uit vergelijking (m_1) volgt dat \(m_1\) niet met de zwaartekracht aan \(m_2\) trekt! De massa \(m_1\) versnelt, waarvoor een resulterende kracht nodig is.
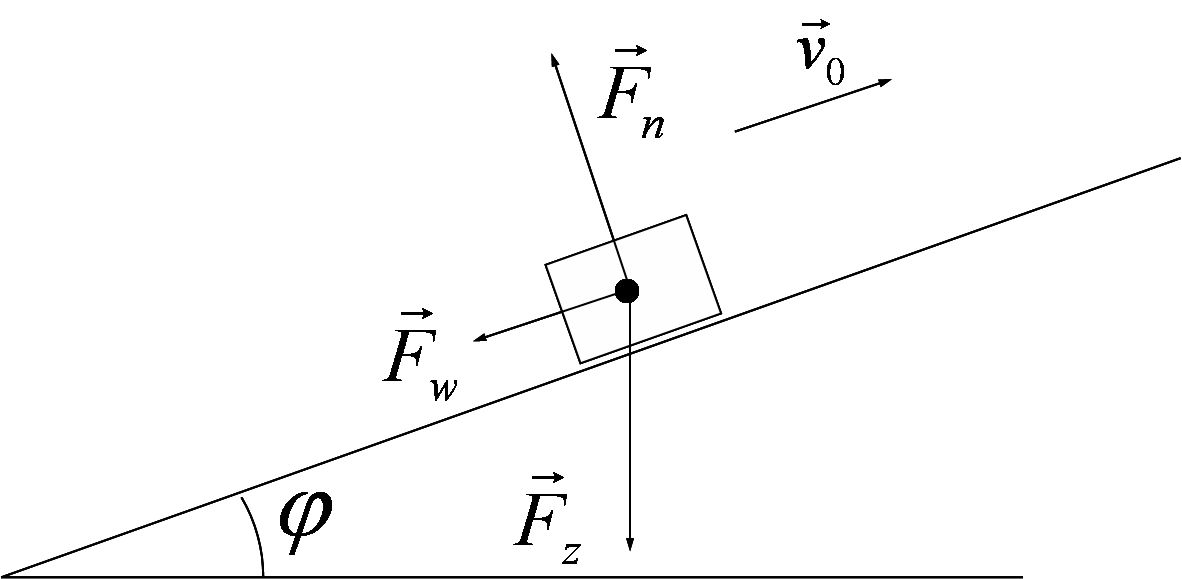
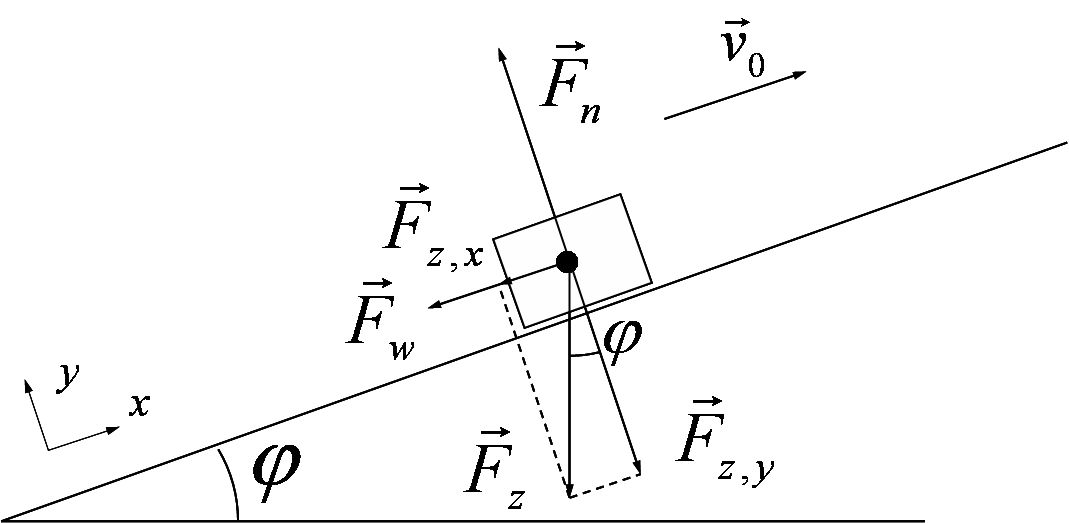
\(a=-\frac {F_w+mg\sin \varphi }{m}=\SI {-8,66}{m/s^2}\)
\(x=-\frac {v_0^2}{2a}=\frac {mv_0^2}{2(F_w+mg\sin \varphi )}=\SI {3,70}{m}\)
\(F_{zx}>F_w\) zodat het blok terug naar beneden komt.
\(\mu =\frac {F_w}{mg\cos \varphi }=0,44\)