Je bent je ingevulde velden bij deze pagina aan het verwijderen. Ben je zeker dat je dit wilt doen?
You are erasing your filled-in fields on this page. Are you sure that is what you want?
Nieuwe Versie BeschikbaarNew Version Available
Er is een update van deze pagina. Als je update naar de meest recente versie, verlies je mogelijk je huidige antwoorden voor deze pagina. Hoe wil je verdergaan ?
There is an updated version of this page. If you update to the most recent version, then your current progress on this page will be erased. Regardless, your record of completion will remain. How would you like to proceed?
Deze open-source cursus is in ontwikkeling. De aanbevelingen van leerlingen om
dit materiaal te verbeteren zijn erg welkom via info@wiskunde.opmaat.org Dit kan gaan over:
Een voorbeeld dat onduidelijk is.
Onnauwkeurigheden, schrijffouten, ...
Een tussenstap die beter uitgelegd moet worden.
Een uitleg die je op youtube, wikipedia of aan de kersttafel gevonden hebt
die ophelderend was.
...
Als je met een keu tegen een biljartbal stoot, vliegt de bal vooruit. We kennen
niet zomaar de ervaring waar de bal dat uit zichzelf doet; de stoot is nodig
om de bal in beweging te brengen. De overgang van rust naar beweging is
m.a.w. het gevolg van de stoot of de stoot is te zien als de oorzaak van de
bewegingsverandering. De ontstane beweging is dan ook te verklaren vanuit de
stoot.
Voor de moderne wetenschap is deze beschrijving en verklaring echter niet voldoende. (Voor Aristoteles (384-322 v.C.) waren vier oorzaken nodig om de werkelijkheid
te kunnen verklaren. Ten eerste heeft de biljartbal een materiële oorzaak. Zonder
materie is er geen bal. Ten tweede moet er een formele of vormelijke oorzaak. De bal
is rond of het zou niet over een biljartbal kunnen gaan; de vorm is essentieel om over
een bal te kunnen spreken. Bovendien kan materie niet zonder vorm bestaan. Ten
derde moet er een bewerkende oorzaak zijn; de beweging van de bal is het gevolg van
de stoot met de keu. Als laatste oorzaak moet er een doeloorzaak zijn. De beweging
vindt maar plaats met een bepaald doel, nl. het willen potten van de bal. Het is
maar omdat je de bal wilt potten dat de beweging plaatsvindt. Niemand
zal met keus in het wilde weg beginnen stoten tegen ballen op biljarttafels.
Daarvoor moet bovendien al het spel eerst gemaakt worden met het oog op
ontspanning.)
Ze is enkel kwalitatief. Dat wil zeggen, ze beschrijft het verschijnsel slechts in
algemene termen maar niet in meetbare grootheden. Voor de beschrijving willen we
niet alleen weten dát de bal beweegt maar ook hóe ze dat doet. Voor de verklaring is
een ‘stoot geven’ niet genoeg, we willen uit de grootte van de kracht en uit de hoek
waaronder dit gebeurt, kunnen berekenen hoe de bal vooruit zal gaan. Willen we
dus iets verklaren dan hebben we nood aan een kwantitatieve beschrijving
en verklaring. De beweging moeten we met meetbare grootheden kunnen
uitdrukken en de fysische wetmatigheid die de relatie tussen kracht en de
daaruit volgende beweging geeft, moet in formulevorm uit te drukken zijn.
(Voor de moderne wetenschap is zeker de doeloorzaak niet meer van
toepassing. We verklaren niet in termen van ‘waarom’ maar eerder met ‘waardoor’.
Een bijkomend en cruciaal element is ook de vraag naar een kwantitatieve
beschrijving.)
Als de kracht de oorzaak is van de bewegingsverandering, hoe zit het dan precies met
die relatie? Gegeven een kracht, wat is dan de beweging? Om deze vraag deels (Het volledige antwoord is terug te vinden in hoofdstuk debeginselenvannewton.) te beantwoorden bekijken
we drie voorbeelden.
Als je stopt met trappen op de fiets, bol je uit. Je zou dit kunnen verklaren door te
stellen dat voorwerpen naar rust streven. Deze verklaring loopt echter al snel mank
wanneer je ze wil toepassen op bijvoorbeeld de Voyager 1. Deze ruimtesonde bevindt
zich bijna buiten ons zonnestelsel en vliegt met een duizelingwekkende snelheid van
meer dan \(61\,000\) \(\mathrm {km}\,\mathrm {h}^{-1}\) de interstellaire ruimte tegemoet. Ze valt niet stil en heeft bovendien geen
brandstof nodig om voort te blijven gaan. Het uitbollen met de fiets en het blijven
voortgaan van de ruimtesonde verklaren we met de wet van de traagheid.
Wanneer je stopt met trappen wil je de verkregen beweging aanhouden maar
de wrijvingskracht houdt dit tegen. In de ruimte is er geen wrijving zodat
objecten kunnen blijven bewegen, zonder dat daarvoor een kracht nodig
is.
Figuur 1: Experimenteel bekomen grafieken van een verticale worp
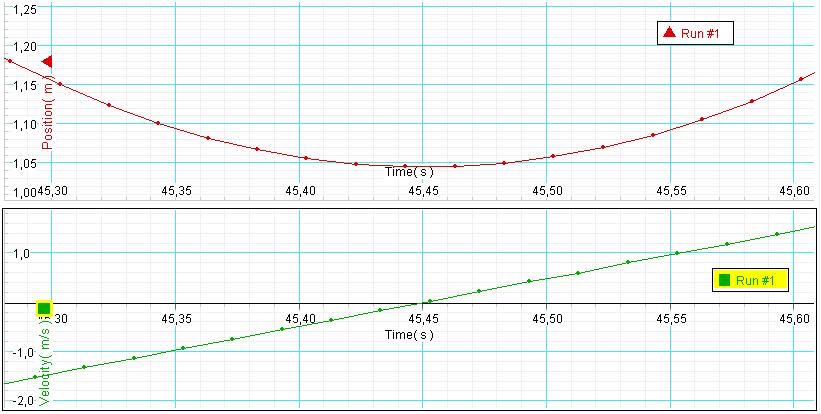
Als we een appel laten vallen zal de zwaartekracht ervoor zorgen dat de appel naar de
aarde valt. Wanneer we bovendien de snelheid meten, zien we dat deze snelheid
toeneemt en wel op een constante manier. Dat wilt zeggen dat de verandering in
snelheid steeds gelijk is. Er komt per tijdseenheid steeds evenveel snelheid bij. De
appel valt sneller en sneller, maar de mate waarin dat gebeurt, is constant. Gooien
we hem op, dan zien we dat zwaartekracht en snelheid een tegengestelde zin hebben.
De zwaartekracht zorgt dus duidelijk niet voor de beweging omhoog (de appel blijft
omhoog gaan) maar voor een vertraging van de beweging. De snelheid waarmee de
appel omhoog beweegt, neemt af. Ook hier zien we – nadat we meten – dat de
snelheid gelijkmatig afneemt. De snelheid waarmee de appel per tijdseenheid
afneemt, is steeds gelijk. Of de appel nu snel gaat of traag, de mate van
afname is steeds gelijk. We kunnen dus concluderen dat de zwaartekracht
voor een verandering van bewegingstoestand zorgt; de snelheid blijft niet
hetzelfde. We zien zelfs dat die verandering van de snelheid gelijkmatig is. De
constante zwaartekracht zorgt blijkbaar voor een constante verandering van de
snelheid.
Als je kijkt naar een koppel schoonschaatsers, dan zie je naast een fantastische
prestatie en een mooi schouwspel, dat een kracht niet altijd voor een toename of
afname in de grootte van de snelheid hoeft te zorgen.
Figuur 2: Een prachtig schouwspel...
De jongen in de figuur moet duidelijk een kracht uitoefenen om het meisje dat rond
hem draait, bij te houden. De kracht die nu wordt uitgeoefend, dient niet zozeer voor
het veranderen van de grootte van de snelheid dan wel voor het veranderen
van de richting van de snelheid. Op elk moment verandert de richting van
de snelheid, en dit naar de jongen toe – volgens de richting en zin van de
kracht.
We kunnen concluderen dat een kracht niet zozeer invloed uitoefent op de snelheid
dan wel op de verandering van de snelheid. Deze verandering houdt zowel een
verandering van grootte en/of een verandering van richting in. Bovendien blijkt uit de
laatste twee voorbeelden dat de verandering te associëren is met de kracht; de
verandering is in de richting en zin van de kracht. Snelheid is te beschrijven als
een vector en verandering van grootte en/of richting vallen beide onder het
veranderen van de vector. Als we die verandering versnelling noemen, lijkt er een
relatie te zijn tussen de kracht en de versnelling – tussen de oorzaak en het
gevolg…
In hoofdstuk \(1\) bekijken we vectoren als voorkennis om fysische objecten te beschrijven.
In hoofdstuk \(2\), \(3\) en \(4\) bekijken we het formalisme om bewegingen te beschrijven. Dit
onderdeel noemen we kinematica. In hoofdstuk 5 en 6 behandelen we dan het
verklarende principe achter de beweging. Dit noemen we dynamica. Het geheel –
kinematica en dynamica – noemen we mechanica.
Semester 1
