Je bent je ingevulde velden bij deze pagina aan het verwijderen. Ben je zeker dat je dit wilt doen?
You are erasing your filled-in fields on this page. Are you sure that is what you want?
Nieuwe Versie BeschikbaarNew Version Available
Er is een update van deze pagina. Als je update naar de meest recente versie, verlies je mogelijk je huidige antwoorden voor deze pagina. Hoe wil je verdergaan ?
There is an updated version of this page. If you update to the most recent version, then your current progress on this page will be erased. Regardless, your record of completion will remain. How would you like to proceed?
De eerste wet vertelt ons niet volledig wat er gebeurt wanneer op een lichaam een
kracht werkt. Ze vertelt ons niet wat de relatie tussen kracht en beweging is. Dat
doet de tweede wet.
Een bal waar je harder tegen schopt, krijgt een grotere snelheid mee en een
pingpongballetje vliegt gemakkelijker weg dan een basketbal wanneer je er een tik
tegen geeft. Als je het nader onderzoekt, door bijvoorbeeld verschillende krachten
op een wagentje met eventueel steeds andere massa’s te laten inwerken en
de bijbehorende versnellingen te meten, merk je dat de versnelling recht
evenredig is met de resulterende kracht en dat massa en versnelling omgekeerd
evenredig zijn. M.a.w. \(a\sim F/m\). Als bovendien een kracht zijdelings inwerkt op een
bewegend voorwerp, dan merk je dat de baan afbuigt, in de richting van de
kracht.
De eenheid van de grootheid kracht is de newton (symbool N). Eén newton wordt
gedefinieerd als de grootte van de kracht die een massa van één kilogram een
versnelling van één meter per seconde kwadraat geeft.
Bovenstaande observaties, samen met de definitie van de eenheid van kracht, zitten
vervat in de tweede wet van Newton, die een kwantitatieve relatie tussen kracht en
versnelling poneert.
De tweede wet van Newton ˙
De versnelling van een voorwerp is recht evenredig met de erop inwerkende
resulterende kracht en omgekeerd evenredig met de massa van het voorwerp. In
symbolen:
De wet spreekt over de resulterende kracht. Het is de resulterende kracht die gelijk is
aan \(m\vec {a}\), niet zomaar een van de inwerkende krachten.
Het gaat over de resulterende kracht die op het voorwerp met massa \(m\) wordt
uitgeoefend en over de versnelling \(a\)van het voorwerp. De krachten worden door
andere voorwerpen op het voorwerp uitgeoefend. Het is niet dat het voorwerp een
kracht ‘bezit’ of een kracht op zichzelf kan uitoefenen.
De formulevorm is een vectorvergelijking. Zoals de kracht is, is ook de versnelling.
Omdat de formule een vectorvergelijking is, is de gegeven formule equivalent met de
componentsvergelijkingen:
De componentsvergelijkingen zijn in de praktijk handiger,
er valt algebraïsch mee te rekenen.
De tweede bewegingswet geeft een verband tussen de oorzaak van een beweging (de
resulterende kracht) en de versnelling van de beweging.
De formulevorm van de tweede wet ziet er misschien gemakkelijk uit maar is in al
haar eenvoud immens krachtig. De wetmatigheid verklaart alle mechanische
bewegingen; als we de krachten kennen, kennen we de versnelling van het voorwerp
en kunnen we (althans op zijn minst in theorie) de baan van het voorwerp
bepalen.
In feite zit de eerste wet vervat in de tweede. Toch blijven we hem gebruiken, vooral
om het concept traagheid te benadrukken.
Denkvraag 1
Waar en hoe in het filmpje van Wile E. Coyote en de Road Runner wordt de tweede
wet van Newton met de voeten getreden?
Een massa van \(2\mathord {,}0\) \(\mathrm {kg}\) bevindt zich in een lift aan een dynamometer. Die laatste duidt
een kracht van \(10\) \(\mathrm {N}\) aan. Welke beweging voert de lift uit?
De lift beweegt naar omlaag met een versnelling van \(5\mathord {,}0\) \(\mathrm {m}/\mathrm {s}^{2}\). De lift beweegt naar omhoog met een versnelling van \(5\mathord {,}0\) \(\mathrm {m}/\mathrm {s}^{2}\). De lift beweegt naar omlaag met een constante snelheid. De lift beweegt naar omhoog met een constante snelheid.
Op een luchthaven trekt een vrouw haar koffer met een constante snelheid voort.
Het handvat maakt een hoek \(\theta \) met de horizontale. De massa van de koffer is \(10\mathord {,}5\) \(\mathrm {kg}\). De
vrouw trekt volgens de richting van het handvat met een kracht van \(25\mathord {,}0\) \(\mathrm {N}\) terwijl de
grootte van de wrijvingskracht op de valies \(11\mathord {,}0\) \(\mathrm {N}\) bedraagt.
(a)
Teken het krachtendiagram van de koffer.
(b)
Bepaal de hoek \(\theta \) tussen het handvat en de
horizontale.
(c)
Bepaal de normaalkracht die de grond op de koffer
uitoefent.
De snelheid
is constant zodat volgens de horizontale richting de versnelling nul is. De component
van de trekkracht volgens deze richting moet dan ook even groot zijn als de
wrijvingskracht:
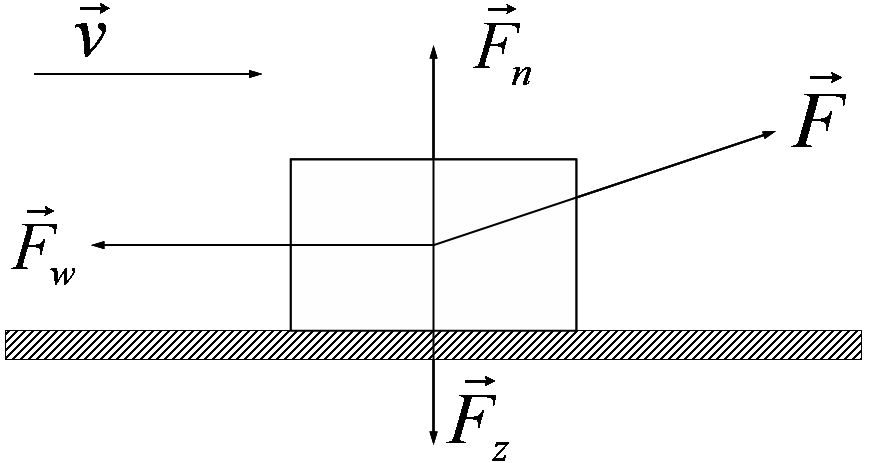
Ook volgens de verticale richting is de versnelling nul zodat (Als je expliciet het
gevraagde in functie van de gegevens wil zetten, moet je de \(y\)-component van de
trekkracht met de stelling van Pythagoras berekenen. De uitkomst is dan \(F_n=mg-\sqrt {F^2-F_w^2}\).) :
In de laadruimte van een vrachtwagen hangt een slinger aan het plafond vast.
Doordat de vrachtwagen met een constante versnelling optrekt, maakt het touw van
de slinger een hoek van \(\SI {37}{\degree }\) met de verticale.
Bepaal de grootte van de versnelling van de vrachtwagen.
Onder invloed van een kracht \(\vec {F}\) beweegt een blok met constante snelheid over een
ruw horizontaal oppervlak. De krachten op de figuur hebben de juiste oriëntatie maar
niet noodzakelijk de juiste grootte. Welke van de volgende relaties tussen \(\vec {F}\), \(\vec {F}_w\), \(\vec {F}_z\) en \(\vec {F}_n\) moet
in ieder geval waar zijn?
\(F_w=F\) en \(F_n=F_z\)\(F_w<F\) en \(F_n<F_z\)\(F_w=F\) en \(F_n>F_z\)\(F_w<F\) en \(F_n=F_z\)
We ontbinden de kracht \(\vec {F}\) in zijn twee componenten volgens de horizontale en
verticale richting: \(\vec {F}_x,\vec {F}_y\). Aangezien het blok in de verticale richting niet versnelt, moet \(F_z=F_n+F_y\) of \(F_n<F_z\).
Semester 1
