 Semester 1
Semester 1- Verberg vooruitgang Hide progress Toon vooruitgang Show progress
- Verwijder je antwoorden (op deze pagina) Remove your answers (on this page)
 Semester 1
Semester 1Deze open-source cursus is in ontwikkeling. De aanbevelingen van leerlingen om
dit materiaal te verbeteren zijn erg welkom via info@wiskunde.opmaat.org
Dit kan gaan over:
Algemeen zal een kracht gedurende de verplaatsing niet constant blijven. Ze zal met andere woorden o.a. afhankelijk zijn van de plaats waar het lichaam zich bevindt. We kunnen die afhankelijkheid beschrijven met behulp van een functie, de (grootte van de) kracht als functie van de plaats:
Eenvoudigheidshalve beperken we ons hier tot bewegingen op een rechte. Bewegingen in meerdere dimensies vereisen een uitgebreidere integraaltheorie dan hetgeen we nu kennen.
We geven een opbouw om tot een definitie van arbeid te komen in het geval dat de kracht dus niet constant is. Ze vertoont gelijkenissen met de opbouw van de integraal.
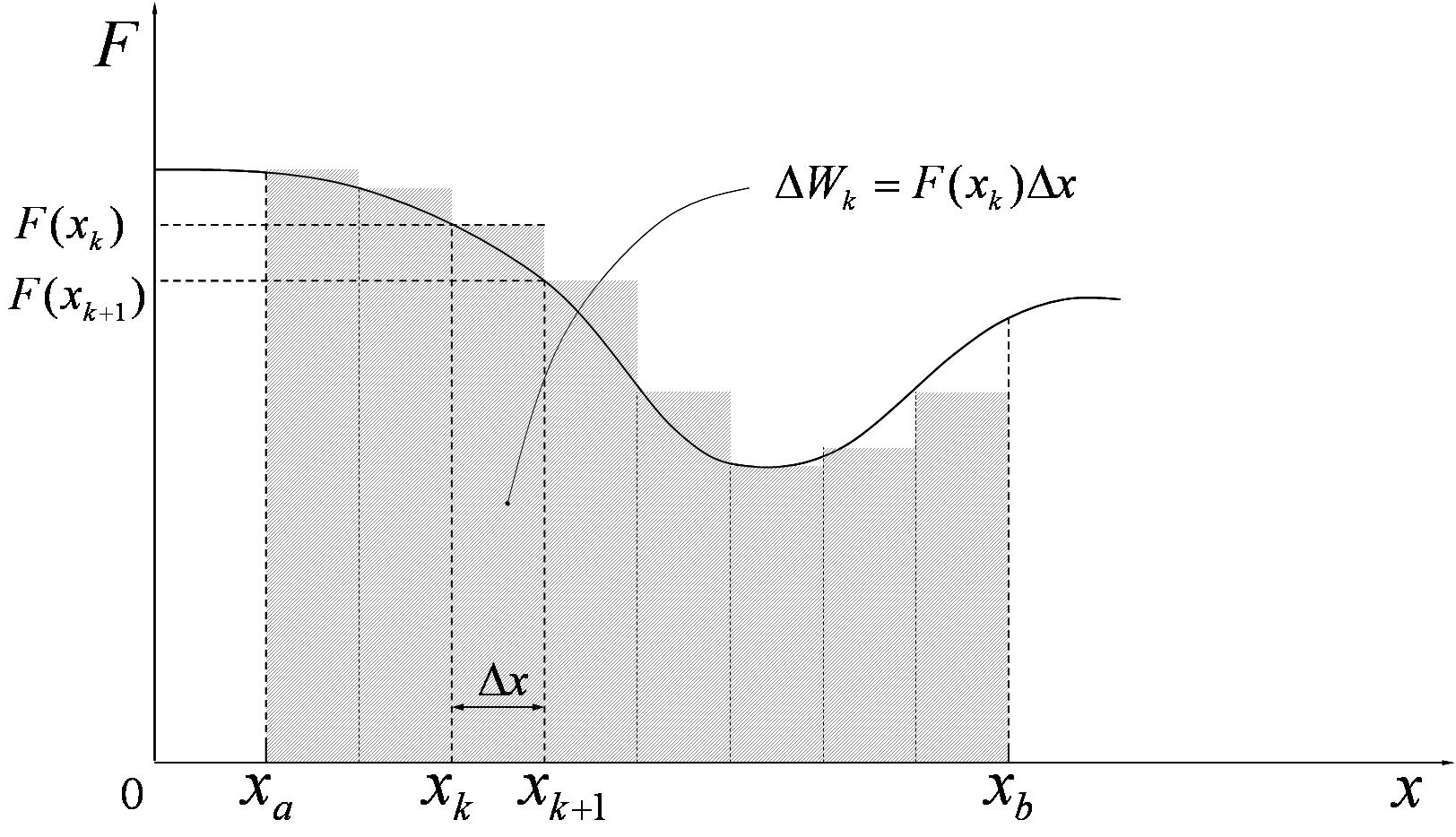
Verdeel de verplaatsing \(x_b-x_a\) in heel veel hele kleine stukjes \(\Delta x\) bijvoorbeeld als volgt:
met \(n\in \mathbb {N}_0\) zeer groot. De posities tussen de stukjes kunnen we dan beschrijven door
Hoe kleiner \(\Delta x\) is, hoe minder de kracht binnen deze stukjes variëert en hoe meer dus \(F(x_k)\) de kracht weergeeft die aanwezig is bij de verplaatsing van \(x_{k}\) naar \(x_{k+1}\). Het kleine stukje arbeid \(\Delta W_k=F(x_k)\Delta x\) zouden we kunnen beschouwen als een benadering van de geleverde arbeid gedurende deze kleine verplaatsing. De arbeid geleverd bij de gehele verplaatsing zou dan overeen kunnen komen met de som van alle stukjes geleverde arbeid. Hoe kleiner we \(\Delta x\) nemen hoe meer die som overeenkomt met wat de totale arbeid zou moeten zijn, vandaar dat in de limiet van \(\Delta x\) gaande naar nul, we de geleverde arbeid zouden kunnen vinden. Deze limiet komt overeen met het nemen van een integraal:
Dit moet de volgende algemene definitie van arbeid legitimeren.
De mechanische arbeid \(W\), geleverd door een kracht \(\vec {F}(x)\) gedurende de verplaatsing op een rechte van \(x_a\) tot \(x_b\) wordt gedefinieerd als
waarbij \(F_x(x)\) de getalcomponent van \(\vec {F}(x)\) is volgens de bewegingsrichting.
Opmerkingen:
| Voorbeeld: Arbeid door een veer geleverd |
Een eenvoudig maar duidelijk voorbeeld van een kracht die afhankelijk is van de plaats is
de kracht door een veer uitgeoefend. Voor niet te grote uitwijkingen wordt deze gegeven
door de wet van Hooke:
Hierin is \(k\) de veerconstante en \(x\) de verlenging van de veer t.o.v. zijn evenwichtspositie . Het minteken komt van het feit dat de kracht steeds tegengesteld is aan de uitwijking. Het is een terugroepkracht. Bij het samendrukken van de veer bijvoorbeeld is \(x<0\) zodat de kracht positief en dus tegengesteld aan de uitwijking is.

We willen de arbeid berekenen door de veerkracht geleverd op een massa bij de verplaatsing van een verlenging \(x_a\) naar een verlenging \(x_b\). Volgens de definitie wordt dit:
Indien het beginpunt \(x_a\) verder uit de evenwichtspositie ligt dan het eindpunt \(x_b\) is de
geleverde arbeid positief.