 Semester 1
Semester 1- Verberg vooruitgang Hide progress Toon vooruitgang Show progress
- Verwijder je antwoorden (op deze pagina) Remove your answers (on this page)
 Semester 1
Semester 1Deze open-source cursus is in ontwikkeling. De aanbevelingen van leerlingen om
dit materiaal te verbeteren zijn erg welkom via info@wiskunde.opmaat.org
Dit kan gaan over:
Beschouw een massa onderhevig aan de universele gravitatiekracht. We gaan opnieuw opzoek naar een potentiële energiefunctie geassocieerd aan deze kracht.
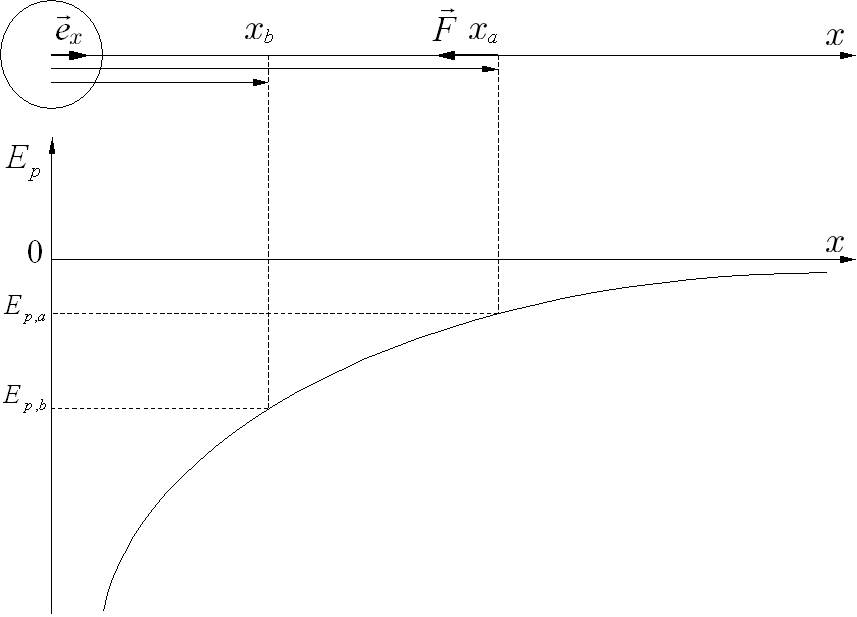
Kiezen we een \(x\)-as met de oorsprong op de massa \(m\) dan wordt, omdat de kracht steeds naar de oorsprong is gericht, de component van de universele gravitatiekracht op de massa \(m'\) gegeven door
De arbeid die door de gravitatiekracht wordt geleverd bij de verplaatsing van de massa \(m'\) van \(x_a\) naar \(x_b\) wordt dan:
De potentiële energie voor een massa \(m'\) wordt bijgevolg geven door